
Hubble Spectroscopy of the Blue Star Cluster Containing the Supermassive Black Hole in Andromeda |
|---|
A central dark object "weighing" -- we estimated -- as much as (20 to 80) million Suns was discovered in the center of the Andromeda Galaxy in two independent studies, Kormendy (1987, in IAU Symposium 127, Structure and Dynamics of Elliptical Galaxies, ed. de Zeeuw, Reidel, 17 and 1988, ApJ, 325, 128) and Dressler & Richstone (1988, ApJ, 324, 701) Both studies suggested that the dark object is a supermassive black hole. This was the second of what are now about 40 detections of central dark objects in galaxies. All are believed to be supermassive black holes; that is, dead relics of quasars. The heyday of quasars was 10 to 13 billion years ago. Now, almost all of them have switched off, because they are no longer being fed by infalling gas and stars. A major success of our paradigm that quasars are powered by supermassive black holes is the observation that the nearby dark objects in galactic centers -- objects like the one in Andromeda -- add up to the right mass to account for the enormous energy output of quasars.
But there has always been an important uncertainty. When we detect a central dark object by measuring how fast stars revolve around it, we cannot tell directly what the dark object is made of. Supermassive black holes are one of several possibilities. An alternative possibility is a cluster of dark stars -- either "brown dwarf" stars that are too low in mass to ignite the nuclear reactions that make stars shine or "white dwarf" stars, "neutron stars" or stellar-mass black holes that are the dead remnants of high-mass ordinary stars. Such dark clusters have always been implausible, because the extreme kind of star formation required to produce them has never been observed. But discovery of a supermassive black hole is an extreme claim, and extreme claims require extremely good evidence. So a high priority has always been to test rigorously whether a dark cluster alternative to a supermassive black hole is possible. Now, Bender et al. (2005, ApJ, 631, 280) have made this test. It turns out that making a dark cluster alternative to a supermassive black hole in Andromeda violates either the observations or the physics of stars.
Since 1988, the Andromeda galaxy has been re-observed repeatedly with better and better spatial resolution (for a complete list and review, see Kormendy (2004, in Carnegie Observatories Astrophysics Series, Volume 1, Coevolution of Black Holes and Galaxies, ed. Ho, Cambridge University Press, 1. These studies have confirmed the detection of the dark object and refined its mass measurement. But the mass has remained uncertain, because of the complicated structure of the galaxy's nucleus.

Lauer et al. (1993, AJ, 106, 1436) used the Hubble Space Telescope to discover that the nucleus of the galaxy is double. This is a color image of the double nucleus constructed from Hubble WFPC2 exposures in near-infrared, green, and ultraviolet light obtained by Lauer et al. (1998, AJ, 116, 2263). The left brightness peak (with embedded blue light source) is called P2; the right peak is called P1. The infrared and green images were substepped by half of a PC pixel, so the scale is 0.0228 arcsec/pixel. This figure is from Kormendy and Bender (1999, ApJ, 522, 772). In this paper, we present arguments that the blue source is a star cluster and that the supermassive black hole is embedded in it. Photo credit: John Kormendy (University of Texas at Austin) and Ralf Bender (University Observatory, Munich, Germany)
The double nucleus is hard to understand. The simplest explanation is almost certainly wrong. The picture above shows what look like two star clusters in orbit around each other. Galaxy collisions and mergers are common. It is natural to wonder whether we are seeing the last stages of such a collision, when the remnants of the nuclei of the two progenitor galaxies are about to merge. The trouble is this: Two clusters in orbit around each other at a projected separation of 0.5 arcsec = 6 light years would merge in less than 100 million years. This sounds like a long time, but it is embarrassigly short. The stars in the clusters are many billions of years old. It is very unlikely that we would catch the galaxy at just the brief moment when its two nuclei have almost but not quite merged.
Tremaine (1995, AJ, 110, 628) proposed what is now the standard explanation. He suggested that both red nuclei are parts of the same eccentric disk of stars with the black hole at one focus. The brighter nucleus, P1, is farther from the black hole and results from the fact that stars in very elongated orbits move slowly when they are farthest from the black hole. They linger for a long time at these radii and make the bright spot that we see as P1. The fainter nucleus, P2, is explained by increasing the disk density toward the center. A black hole is required to make this explanation work; otherwise, the elongated orbits will not stay lined up and pointing at P1. This explanation is well illustrated by artist's conceptions and a movie posted in the press release from NASA and the Space Telescope Science Institute. Is it correct? Kormendy & Bender (1999, ApJ, 522, 772) show that observations of the double nucleus strongly support Tremaine's eccentric disk model.
Why is this important for the black hole problem? First, the non-circular stellar orbits in the eccentric disk make it harder to estimate the mass of the black hole. Second, the eccentric disk is still big enough so that dark cluster alternatives to a supermassive black hole are not excluded (Maoz 1998, ApJ, 494, L181).

Studying the blue light source in P2 solves these problems. Bender et al. (2005, ApJ, 631, 280) have observed the double nucleus and embedded blue source with the Space Telescope Imaging Spectrograph (STIS). The slit positions are shown above, superposed on Hubble images. Click on the picture to get a bigger version. The left panel shows the 0.1 arcsec slit used to measure the red light of the double nucleus. The image was taken through a green filter and just barely shows the blue source. Farther into the red where the spectra were taken, the blue nucleus is invisible. So this spectrum measures the red double nucleus with no contamination from the blue source. The right panel shows the 0.2 arcsec slit used for the blue source. This image was taken through an ultraviolet filter; at these short wavelengths, the blue source is much brighter than the red stars. In our blue spectrum, it is bright enough so that we can correct easily for the small contamination from red stars. As a result, we get a clean spectrum of the blue light source without any residual contribution from the red stars.
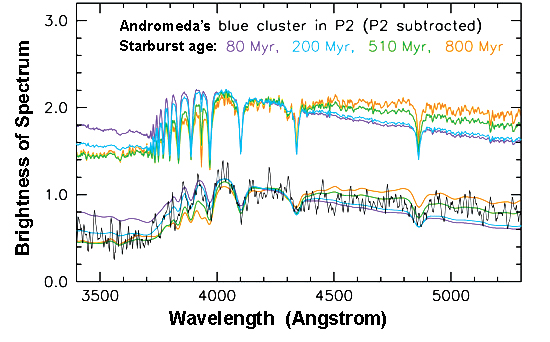
The black line above shows the spectrum of the blue source. The figure shows its brightness at each wavelength (or color) in arbitrary units plotted against wavelength. For example, 5000 Angstrom light looks green to our eyes, 4600 Angstrom light looks blue, and 4200 Angstrom light looks violet. The small-scale wiggles in the spectrum are noise in the measurements. But the broader dips in brightness at 4856, 4336, 4097, 3966, and 3885 Angstrom are real. The sharp blueward drop in brightness at about 3800 Angstrom is real, too. These features are well known -- they are the spectrum of hydrogen gas as measured in the laboratory on Earth. Spectra of stars show exactly these dark lines of hydrogen provided that the surface temperature is about 10,000 degrees K. An example of such a star is Sirius, the brightest star in the night sky as seen from Earth. Sirius matches the spectrum of the blue source very well. So the spectrum in the above figure proves that the blue source is a cluster of hot stars.
It also tells us the ages of the stars. Hot stars like Sirius use up their nuclear fuel quickly. They live only a few hundred million years. So the cluster is young. We estimate its age by fitting the observations (black line) with the spectra of stars in starbursts of ages 80, 200, 510, and 800 million years (colored lines). Younger starbursts have more hot, blue stars and so look brighter at blue wavelengths and fainter at red wavelengths. Also, by the time the starburst is 800 million years old, the hot stars that show hydrogen lines have begun to die and these lines get weaker. We get our best fit to the spectrum when the starburst is 200 million years old.
Young stars so close to a supermassive black hole are a major puzzle, as highlighted in the press release from NASA and the Space Telescope Science Institute Stars near the black hole must whizz around it much faster than stars farther out (see the videos posted with the Space Telescope press release. The movie zooms in on the center; you need to wait until the end to see the spinning disk of blue stars.) The same is true of any gas disk that, presumably about 200 million years ago, was trying to form stars. It is hard to understand how such a disk could be unstable. How could it collapse under its own gravity and make stars? After all, it is ferociously sheared by the gravity of the black hole. How the blue stars formed is a major mystery.
But the stars are there. Even without understanding their origin, we can easily use them to measure the mass of the black hole:
The above figure shows the raw starburst spectra at the top. Notice that the dark features are narrow. The fits to the blue cluster shown at the bottom of the figure include one more detail that was not mentioned above. The starburst spectra have been shifted slightly in wavelength to take into account the 300 km/s motion of the Andromeda galaxy toward us. They have also been broadened to fit the wide dips in brightness observed in the spectrum of the blue cluster. The broadening is caused by the Doppler effect -- the stretching (redshift) of the wavelength when the source is moving away from us and the compression (blueshift) of the wavelength when it is moving toward us. Some stars in the nucleus move toward us, some move away from us, and the result is a widening of the spectral features. By matching this widening, we can measure how fast the stars are moving. We conclude that the blue stars typically move at about 1100 km/s. In contrast, the red stars in the same direction move at only about 250 km/s. This proves that the supermassive black hole is inside the blue cluster.
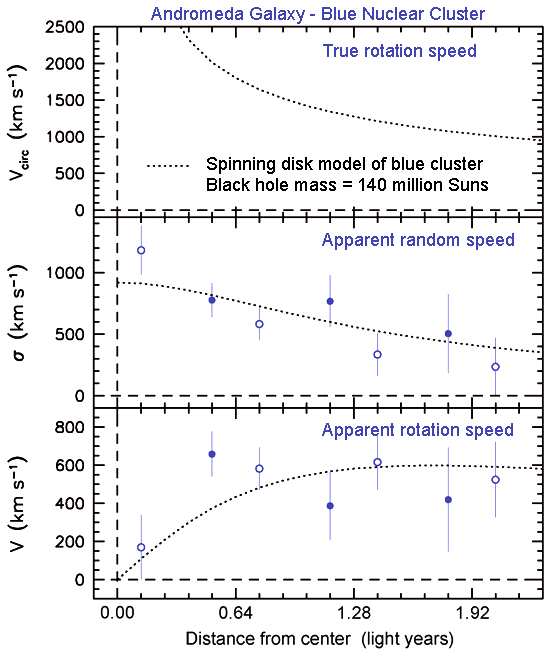
We can go one step further. We can measure the Doppler shift and the Doppler broadening of the spectral features in the blue cluster at various radii from the center. The results are shown above. The bottom panel shows rotation speed. We observe that the blue cluster rotates at about 600 km/s at a radius of about one-half of a light year; from this value, the rotation speed drops slowly outward. The middle panel shows the random speeds of the stars. They are the highest such speeds seen in any galaxy except our own. They, too, drop outward. Both observations tell us that a big mass sits at the center, pulling gravitationally on the stars. But the light that we measure has been blurred by the telescope -- less than it would be from the surface of the Earth, but still significantly. Also, the large slit width and CCD detector pixels smear the light. The bottom two panels include the effects of this smearing. The real rotation of the cluster is much faster than what we observe. In fact, we are forced to conclude that the blue cluster is a spinning disk of stars with the rotation speeds shown in the top panel of the figure and with essentially zero random speeds. The big apparent random speeds are blurred rotation. For example, the random speed at the center looks big, almost 1200 km/s. But at these small radii, we mix light from stars that are moving toward us on one side of the center with light from stars that are moving away from us on the other side of the center. So we see a wide spectral dip in brightness but no shift. It is easy to calculate this effect and to correct for it.
This calculation gives us the true rotation speeds of the blue cluster -- which we now know is a blue disk -- as a function of radius. They are shown in the top panel of the above figure. The disk spins very quickly. At one-half of a light year, the stars are moving at about 2000 km/s and revolve once around the black hole in about 500 years!
We can now calculate the black hole mass. It is equal to the square of the rotation speed times the radius of the stellar orbits divided by the gravitational constant (tabulated in many references). The black hole mass is 140,000,000 Suns. This is two or three times bigger than we thought from less accurate analyses of the red stars.
The new observations dramatically strengthen the evidence that the central dark object in Andromeda is a supermassive black hole. The alternatives -- clusters of millions of dark stars -- get into serious trouble and can be eliminated. Here's how:
First, we emphasize how the blue cluster highlights the problem. If we believe that Andromeda contains a giant black hole, then we do not understand how these stars could form. But suppose that there were no supermassive black hole. Then the center of the galaxy would be a benign place, and it would be easier for infalling gas to form stars. So how can we be sure that lots of stars didn't form near the center over the roughly 10-billion-year history of the the galaxy? If Andromeda somehow formed tiny, dense clusters of stars repeatedly -- as it seems to have done only 200 million years ago -- what would happen? Well, the high-mass stars in each generation would die quickly and leave behind remnants -- white dwarfs, neutron stars, and stellar-mass black holes -- that would soon be dark and that would gradually build a tiny dark cluster at the center of the galaxy. If this happened often enough, it might construct a 140,000,000 solar mass dark object that is not a supermassive black hole. We need to check this possibility. We also need to check a different possibility, which is that the galaxy somehow formed a tiny, dense cluster of failed stars (they are called "brown dwarfs") that are too low in mass to shine as stars.
To check whether these alternatives are viable, we need to know how big the dark cluster can be. Bigger dark clusters get into less trouble. The rotation speeds in the above figure put a strict limit on how big the dark cluster could be. It turns out that about 100 million solar masses of dark stuff have to live within one-third of a light year of the center or else we cannot explain the rapid rotation of the blue cluster. Is this possible? The answer turns out to be "No!".

The above figure dramatizes how extreme a situation we have in mind. Shown in black-and-white is the Hubble image of the blue cluster. It is magnified so much that the individual CCD pixels are easily visible. The dark cluster that we are investigating emits no light, but we have illustrated its density distribution in red. Its maximum radius of 1/3 light year is almost exactly the same as the radius of the well known Ring Nebula. The Ring Nebula is a single star that is shedding its outer atmosphere into a planetary nebula as it dies. We need to imagine a cluster of roughly 100,000,000 dead stars inside the volume defined by the Ring Nebula. Let's put it another way. The distance from the Sun to the next nearest star, Proxima Centauri, is 4.3 light years. We have to imagine that, at the center of Andromeda, a dark cluster whose radius is more than 10 times smaller than the distance from the Sun to Proxima Centauri contains 100,000,000 times the mass of our Sun in the form of dead stars or failed stars. So the density of this cluster is roughly 100 billion times higher than the density of stars near the Sun. It is more than a million times bigger than the densities at the centers of globular clusters, the densest stellar systems known. Not surprisingly, attempts to make such an object get into serious trouble. Here are some problems:
Failed stars -- brown dwarfs -- have masses less than 0.08 times the mass of our Sun. Because they are so puny, we need more than a billion of them to make our imagined dark cluster. We have not the slightest hint, either observational or theoretical, that Nature can make so many brown dwarfs, especially not without making visible stars, too. But never mind; we don't want to base our arguments on our ignorance. We have a much stronger proof. We know how big brown dwarfs are. For any hypothetical mass, we can calculate how often every typical brown dwarf collides with another brown dwarf. The answers range from tens of millions years for big brown dwarfs to tens of thousands of years for brown dwarfs with masses like that of the Earth. Early on during the buildup of the dark cluster, colliding brown dwarfs will merge into bigger stars that quickly become luminous. We would see them. Late during the buildup of the dark cluster, the brown dwarfs would collide so violently that they would be destroyed - that is, converted back into gas. So brown dwarfs are strongly excluded.
A cluster of dead stellar remnants is a viable explanation only if their progenitor stars can safely live their lives and deliver their remnants where we need them. It turns out that the stars need to survive inside roughly the limiting radius, 1/3 light year, that we get for the dark cluster. But all relevant progenitor stars are at least as big as the Sun. If we try to pack enough of them into the required small volume, they hit each other. Very quickly, they either get destroyed -- that is, converted back into gas, which is self-defeating -- or they get converted into very high-mass stars. High-mass stars die as supernovae. This causes all sorts of trouble. First, these supernovae would be observed in galaxies that are still forming dark clusters. Second, most of the mass of an exploding star is expelled into its supernova remnant gas cloud. This mass would be lost to the dark cluster that we are trying to build. This is counter-productive. Collisions also cause other problems.
Once progenitor stars live inside an already-partly-completed dark cluster, they deposit their remnants too close to the center. Progenitors are typically about 10 times more massive than their dark remnants. As a result, a process called "dynamical friction" causes them to sink to the center. The dark cluster expands correspondingly. This makes it impossible to arrange that the dark cluster have a density distribution with a fairly sharp outer edge, as we need.
For a large range in masses, white dwarfs are excluded because they would collide with each other, merge into an object that is more massive than the Chandrasekhar limit, and explode as a supernova. This is counter-productive. It is also in conflict with observations, because supernovae in Andromeda would be so bright that they could be seen with the naked eye!
There are other problems, too, but the above discussion captures the essence of the arguments against dark clusters. The most conservative explanation for the remarkably high speeds of stars near the center of Andromeda now is a single supermassive black hole.
Previously, dark clusters had been ruled out in only two galaxies, NGC 4258 and our Milky Way Galaxy (Maoz 1998, ApJ, 494, L181). These two galaxies give us important proof that black holes exist. But both are special cases -- NGC 4258 contains a disk of water masers that we observe with radio telescopes, and our Galactic center is so close that we can follow individual stellar orbits. Andromeda now becomes the third galaxy in which plausible alternatives to a supermassive black hole are excluded. And it is the first galaxy in which we can exclude exotic alternatives to a black hole using Hubble and using the same techniques by which we find most other supermassive black holes.
Looking for black holes always was a primary mission of the Hubble Space Telescope. Nailing the black hole in Andromeda therefore is an important part of its legacy. It makes us much more confident that the other central dark objects detected in galaxies are black holes, too.
Press releases on the above paper:
Astrophysical Journal paper on which this site is based (1.5 Mb PDF):
John Kormendy (kormendy@astro.as.utexas.edu)