

The V/sigma - epsilon diagram for bulges of unbarred and edge-on galaxies (Kormendy & Illingworth 1982). Bulges are shown by orange filled circles; ellipticals are shown by red crosses; arrows indicate upper limits. In the diagram, epsilon is the ellipticity of the galaxy and V/sigma is the ratio of the maximum rotation velocity to the mean velocity dispersion near the center. The orange curve is the "oblate line", V/sigma = [epsilon/(1 - epsilon)]^0.5 (Kormendy 1982a); it describes oblate spheroids that are isotropic and flattened only by rotation. The red curve is the correlation between V/sigma and epsilon that would be expected for a typical amount of anisotropy; similar curves span the lower part of the diagram between the oblate line and the epsilon axis. This figure shows that bulges are very similar to isotropic dynamical models, while giant ellipticals are substantially anisotropic.
In 1975 - 1978, a major revolution occurred in the study of elliptical galaxies. It was discovered that giant ellipticals are not stellar systems with nearly isotropic velocity dispersions that are flattened by rotation; rather, they are essentially nonrotating systems whose dynamics and shapes are controlled by velocity anisotropy. The observational origins of the revolution were papers by Bertola & Capaccioli (1975) and by Illingworth (1977); the theoretical interpretation was by Binney (1976, 1978). Since that time, much of the research on elliptical galaxies has concentrated on exploring the implications of velocity anisotropy.
An important contrasting result was the observation that bulges of disk galaxies do rotate rapidly enough to have nearly isotropic velocity distributions (Kormendy & Illingworth 1982) This result is illustrated in the above figure. Bulges lie slightly below the "oblate line" that describes exactly isotropic systems, but some of the apparent flattening is due to the disk potential. Jarvis & Freeman (1985) showed that isotropic models are a good fit to two of these bulges, NGC 4594 and NGC 7814.
Bulges of barred galaxies rotate still more rapidly than bulges of unbarred galaxies (Kormendy 1982b).
It appeared at first that bulges and ellipticals are substantially different, as the above figure suggests. Soon afterward, it became clear that low-luminosity ellipticals also rotate rapidly (Davies et al. 1983). This was an early sign of physical differences between low- and high-luminosity ellipticals. It is now clear that there is a dichotomy between (1) normal- and low-luminosity ellipticals that rotate rapidly, that are nearly isotropic, oblate-spheroidal, and substantially flattened, that have disky-distorted isophotes, and that are coreless, and (2) giant ellipticals that are essentially nonrotating, that are anisotropic, modestly triaxial, and more nearly spherical, that are boxy-distorted, and that have cuspy cores. The above results suggest that the two kinds of ellipticals have different formation histories.
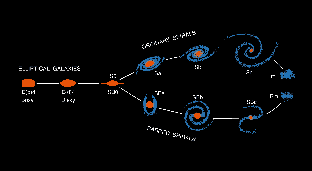
Kormendy & Bender (1996) proposed that the Hubble (1936) classification scheme for E galaxies be revised as shown above, so that it no longer depends on apparent inclination but instead orders ellipticals by isophote shape and hence by fundamental physical properties. Bulges are similar to low-luminosity ellipticals, so the revised Hubble sequence is continuous from disky Es to S0 galaxies to spirals. There may, however, be a physical discontinuity between boxy and disky ellipticals.
Bertola, F., & Capaccioli, M. 1975, ApJ, 200, 439
Binney, J. 1976, MNRAS, 177, 19
Binney, J. 1978, MNRAS, 183, 501
Davies, R. L., et al. 1983, 266, 41
Hubble, E. P. 1936, The Realm of the Nebulae (New Haven: Yale University Press)
Illingworth, G. 1977, ApJ, 218, L43
Jarvis, B. J., & Freeman, K. C. 1985, ApJ, 295, 324
Kormendy, J. 1982a, in Morphology and Dynamics of Galaxies,
Twelfth Advanced Course of the Swiss Society of Astronomy and
Astrophysics, ed. L. Martinet & M. Mayor (Sauverny: Geneva
Observatory), 113
Kormendy, J. 1982b, ApJ, 257, 75
Kormendy, J., & Bender, R. 1996, ApJ, 464, L119
Kormendy, J., & Illingworth, G. 1982, ApJ, 256, 460
University of Texas Astronomy Home Page
John Kormendy (kormendy@astro.as.utexas.edu)